2.3. О сакральной геометрии
В сочинении «Тимей» Платон пишет о мистическом смысле пяти объемных геометрических фигур. Собственно, об этих фигурах было известно и до Платона. Ситуация такая же, как со знаменитой «Теоремой Пифагора», которая была гораздо раньше известна шумерам и египтянам, однако носит его имя.
Платоновы Тела нам будут очень важны для дальнейших пояснений. Они представляют собой выпуклые многогранники, все грани которых – правильные многоугольники. Математически доказывается, что существует именно пять правильных многогранников. Они изображены на рис. 2.4: правильный тетраэдр (1), куб (2), октаэдр (3), додекаэдр (4), икосаэдр (5).
[more]
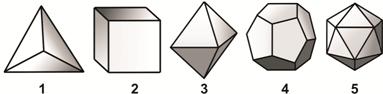
Рис. 2.4. Платоновы Тела
Кратко:
Тетраэдр – имеет 4 одинаковых грани, являющиеся равносторонними треугольниками (одна из граней – основание), 6 ребер и 4 вершины.
Куб – имеет 6 граней (квадратов), 12 ребер, 8 вершин.
Октаэдр – представляет собой бипирамиду, т.е. две четырехгранные пирамиды, сложенные основаниями, имеет 8 граней, 12 ребер и 6 вершин.
Додекаэдр (пентагондодекаэдр) – имеет 12 пятиугольных граней (пентагонов), 30 ребер и 20 вершин.
Икосаэдр – имеет 20 граней, представляющих собой равносторонние треугольники, 30 ребер, 12 вершин.
Хочу привести цитату из http://www.softmixer.com/2014/01/blog-post_9192.html :
…обратимся к Платону. Знаменитый философ называл самым совершенным геометрическим телом додекаэдр – двенадцатигранник, составленный из двенадцати пентагонов. Платон утверждал, что именно его «Бог использовал для планирования Вселенной в качестве образца».
В 2003 году, при анализе данных космического аппарата WMAP, запущенного НАСА, была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре. По данным моделирования, результаты наблюдений свидетельствовали о том, что Вселенная представляет собой набор бесконечно повторяющихся додекаэдров – правильных многогранников, поверхность которых образована 12 пентагонами.
Кстати, пентагон с заключенной в нем пентаграммой был символом знаменитого пифагорейского мистического союза, основанного древнегреческим мыслителем. Так вот, пифагорейцы считали, что их эмблема не только символизирует гармонию Мироздания, но и способна оказывать гармоничное воздействие на окружающее пространство. Границы воздействия, разумеется, зависят от размеров правильного пятиугольника. Так, периметр арлингтонской геометрической фигуры составляет порядка 1405 метров – этого сегодня достаточно, чтобы оказывать влияние на весь мир.
На рис. 2.5 показана связь Платоновых Тел со стихиями.

Рис. 2.5. Платоновы Тела и стихии
Можно видеть, что тетраэдр соответствует огненной стихии, куб – земле, октаэдр – воздуху, икосаэдр – воде, а додекаэдр (его часто называют – пентагондодекаэдр, подчеркивая пентагональность граней) обозначен термином « quinta essentia», что означает – « пятая сущность», в античной философии ее называли «пятый элемент» или (!!!) «эфир»..
Сохраните это в своей памяти. Мы еще вернемся к пентагондодекаэдрам и именно в связи с Космосом.
В заключение этого раздела мне хочется привести выдержки из книги Д. Уилкока «Сдвиг эпох»:
…разные Платоновы Тела четко «гнездятся» внутри друг друга, причем каждая новая геометрия больше, чем находящаяся внутри нее. Характерно, что повышение частоты вовлекает в процесс и увеличение амплитуды.
…точечные концы или вершины Платоновых Тел представляют собой узлы волны. Они находятся там, где во всей сфере создается наименьшее количество вибрации.
В результате мы видим, что в «точках спокойствия» концентрируется огромная энергия, создаваемая давлением окружающих их точек. Узловые области (так же как и центр сферы) обладают самой большой энергетической интенсивностью на всей поверхности сферы, ибо окружающие их зоны высокого давления будут естественно собирать и направлять все «свободное» в зоны точек с низким давлением.
Поэтому, как только формируются узлы, между ними сразу же возникают прямые силовые линии. И когда мы наблюдаем все линии вместе, появляется геометрический объект, просто как результат соединения точек.
