Глава 6: Паттерны удельной теплоты
Рисунок 5: Удельная теплота – Серебро
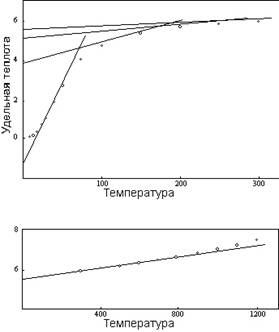
Рисунок 5 – это кривая удельной теплоты, выведенная из экспериментальных данных. Показанные на графике точки являются измеренными величинами удельной теплоты серебра. Сопутствующие сплошные линии - сегменты теоретической кривой для четырех единиц рисунка 4, с эмпирически расположенной температурной шкалой. Хотя определенная точками кривая обладает той же общей формой, что и теоретическая кривая, она очень отличается по виду, потому что острые углы теоретической кривой заменены плавными и постепенными переходами.
Объяснение различия кроется в способе измерения. Как указывалось уравнением 5-8 и кривыми на рисунках 3 и 4, удельную теплоту индивидуальной молекулы можно представить как последовательность прямых линий. Однако экспериментальные наблюдения выполняются не на отдельных молекулах, а не совокупностях молекул. Поэтому наблюдаемая температура совокупности – это средняя температура многих разных индивидуальных молекулярных температур, распределяющихся вокруг средней температуры в соответствии с соображениями вероятности. Среднее между точками перехода отношения между температурой и удельной теплотой для большинства индивидуальных молекул таково, что их удельная теплота лежит на той же прямой линии графика. Таким образом, среднее лежит на той же самой линии и совпадает с истинной молекулярной удельной теплотой, соответствующей средней температуре. Однако по соседству с точкой перехода молекулы, обладающие более высокими температурами, не могут продолжать оставаться на той же линии выше предела 3R, и должны соответствовать нижней кривой, основанной на большем числе вращающихся единиц. Это понижает удельную теплоту совокупности ниже истинной молекулярной величины для превалирующей средней температуры.
Например, у кривой серебра истинная атомная удельная теплота при 75ºК составляет 4,69. Она была бы и средней удельной теплотой совокупности серебра при этой температуре, если бы атомы серебра могли продолжать вибрировать на основе одной единицы вращения вплоть до точки, выше которой вероятностное распределение незначимо. Но при удельной теплоте 2 1/3 R (4,633) вибрация меняется до двух единиц вращения. Атомы в вероятностном распределении, имеющие удельную теплоту выше этого уровня, не могут приспосабливаться к линии одной единицы, и вынуждены следовать линии, которая поднимается с более низкой степенью. Более низкая удельная теплота этих атомов понижает среднюю удельную теплоту совокупности и вынуждает кривую совокупности все больше и больше отклоняться от отношения прямой линии, поскольку пропорция атомов, достигающих точки перехода, возрастает. Отклонение достигает максимума при температуре перехода, после которой удельная теплота совокупности постепенно приближается к верхней атомной кривой. Из-за отклонения измеренной (совокупной) удельной теплоты от величин, относящихся к индивидуальным атомам, удельная теплота серебра при 75ºК составляет 4,10 вместо 4,69.
Аналогичный эффект, но в противоположном направлении, можно видеть на нижнем конце кривой серебра. Здесь удельная теплота совокупности (среднее индивидуальных величин) могла бы оставаться на теоретической кривой одной единицы, только если бы индивидуальная удельная теплота падала ниже нуля. Но здесь нет отрицательной тепловой энергии, и атомы, индивидуально пребывающие при температурах ниже точки, в которой кривая пересекается с нулевым уровнем удельной теплоты, обладают нулевой тепловой энергией и нулевой удельной теплотой. Следовательно, нет отрицательного отклонения от среднего, а положительное отклонение возникает за счет наличия атомов с индивидуальными температурами выше нулевых составляющих удельной теплоты совокупности. Удельная теплота атома серебра при 15ºК равна нулю, но измеренная удельная теплота совокупности серебра при средней температуре 15ºК составляет 0,163.
Оценка отклонения от линейного отношения в областях перехода включает применение математики вероятности, правомочность которой принимается как часть Второго Фундаментального Постулата Обратной Системы. По уже объясненным причинам, полное объяснение аспектов вероятности обсуждаемых явлений выходит за пределы данной работы, но общее рассмотрение ситуации позволит прийти к некоторым качественным выводам, адекватным для нынешних целей.
На современной стадии развития теории вероятности имеется ряд вероятностных функций общего использования, которые, кажется, обладают преимуществами для некоторых применений. В целях данной работы надлежащей функцией является функция, выражающая результаты чистой случайности без модификаций любым другим фактором. Такая функция строго применяется только тогда, когда все вовлеченные единицы точно одинаковы, распределение абсолютно случайно, единицы бесконечно малы, изменчивость непрерывна, а величина группы бесконечно велика. Обычные классы событий, на которых построена самая современная теория вероятности, такие, как эксперименты с монетой и кубиком, очевидно, не удовлетворяют этим требованиям в широком масштабе. Например, монеты меняются не непрерывно с бесконечным числом возможных состояний. У них только два состояния: орел и решка. Это значит, что главное положение неопределенности становится почти определенностью, и форма кривой вероятностного распределения соответственно меняется. Строго говоря, это уже не кривая истинной вероятности, а комбинация кривой вероятности и знания.
Основные физические явления точно удовлетворяют требованиям системы, в которой законы чистой случайности правомочны. Единицы почти однородны, распределение случайно, изменчивость непрерывна или почти непрерывна, а величина группы, хотя и не бесконечна, но крайне велика. Если любую из вероятностных функций общего использования можно принимать как представляющую чистую случайность, самой предпочтительной была бы так называемая функция “обычной” вероятности, которую можно выразить как
|
|
Имеются таблицы этой функции и их интегралы с точностью до пятнадцати десятичных знаков.6 В ходе данной работы было обнаружено, что достаточной точности для нынешних целей можно достичь вычислением вероятностей на основе приведенного выражения. Поэтому ею мы и будем пользоваться во всех применениях вероятности, без необходимости допущения абсолютной точности данной функции в этих применениях или отклонения существования более точных альтернатив. Например, асимметричная вероятность распределения Максвелла точна в применениях, для которых выведена (положение, еще не исследованное в контексте Обратной Системы), и может применяться к некоторым явлениям, обсуждаемым в данной работе. Однако полученные до сих пор результаты, особенно в применении к свойствам жидкостей, говорят в пользу нормальной функции. В любом случае, ясно: Если за счет использования нормальной функции вводится какая-то ошибка, она не так велика, чтобы быть значимой в первом общем подходе к теме.
На этой основе распределение молекул с разными индивидуальными температурами принимает форму вероятностной функции øt, где t – это отклонение от средней температуры. Вклад øt молекул при любой удельной температуре в отклонение удельной теплоты от теоретической величины, соответствующей средней температуре, зависит не только от числа таких молекул, но и от величины отклонения удельной теплоты, приписываемого каждой молекуле. То есть, от разницы между удельной теплотой молекулы и удельной теплотой молекулы при средней температуре совокупности. Поскольку сегмент удельной теплоты, где происходит отклонение, линеен, отклонение пропорционально температурной разнице t и может быть представлено как kt. Общее отклонение, возникающее за счет øt молекул при температуре t равно ktøt, а сумма всех отклонений в одном направлении (положительном или отрицательном) может быть получена путем интегрирования.
Довольно очевидно, что отклонения экспериментальных кривых удельной теплоты от теоретических, прямых линий (и на нулевом уровне, и в точке перехода) обладают общими характеристиками вероятностных кривых. Однако экспериментальные величины не достаточно точные, особенно в области температур низкого перехода, чтобы стоило пытаться проводить любые количественные корреляции между теоретическими и экспериментальными результатами. Более того, еще имеется определенная теоретическая неопределенность в связи с надлежащим применением вероятностной функции, что препятствует установлению точного положения вероятностной кривой.
В данной ситуации, неопределенный элемент – это величина единицы вероятности. Уравнение 6-1 математически завершено, но чтобы применить его или любое из его производных к любой физической ситуации, необходимо установить физическую единицу, соответствующую математической единице. Один из уместных вопросов, еще не имеющий определенного ответа: Является ли единица вероятности одинаковой для всех веществ. Если это так, тогда нижняя часть кривой, будучи понижена до обычной температурной основы, должна быть одинаковой для всех веществ с начальным уровнем 1,32. На этом основании удельная теплота совокупности при температуре T0, когда теоретическая кривая пересекается с нулевой осью, должна быть константой. На самом деле, большинство элементов с начальным уровнем –1,32 обладают измеренной удельной теплотой около 0,20 в этой точке, но некоторые другие демонстрируют значительные отклонения от этой величины. Все еще не ясно, является ли это результатом изменчивости в единицу вероятности или отражает неточности в экспериментальных величинах.
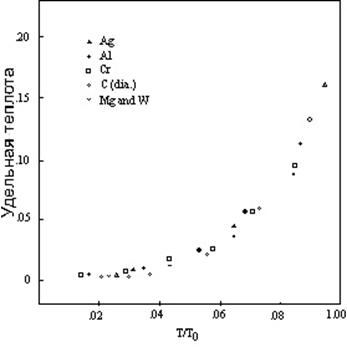
Совпадают ли ниже T0 все кривые с одинаковым максимальным отклонением (0,20), тоже не ясно. Имеется большой разброс и в наблюдаемой удельной теплоте ниже 0,20, который можно приписать ошибкам в измерении, но большую часть разброса, возможно, можно объяснить как результат отсутствия температурного равновесия. На низких температурах для установления равновесия требуется больше времени, и даже точное измерение не даст точного результата до тех пор, пока совокупность не пребывает в температурном равновесии. Значимо, что удельная теплота изученных обычных элементов лишь слегка отклоняется от плавной кривой в области низкой температуры. Рисунок 6 демонстрирует это совпадение, показывая измеренные величины удельной теплоты шести из таких элементов на температурной шкале по отношению к T0.
Если единица вероятности одинакова для всех или большинства элементов, как предполагают эти данные, отклонение экспериментальной кривой от теоретической кривой для единичного атома в точке первого перехода T1, тоже должно быть постоянной величиной. Предварительное исследование кривых элементов, следующих правильным паттернам, указывает на то, что величины отклонения действительно лежат в области приблизительно от 0,55 до около 0,70. Дополнительная работа потребуется прежде, чем эти кривые можно будет установить достаточно точно для того, чтобы определить, существует ли полное совпадение. Современные указания говорят о том, что отклонение T1, на самом деле, является константой для всех обычных элементов и находится рядом с тройным отклонением при T0.
Рисунок 6: Удельная теплота – низкие температуры
Владея вышеприведенной информацией в связи с общей природой отклонений от теоретических кривых главы 5 за счет способа выполнения измерений, сейчас мы готовы исследовать корреляцию между теоретическими кривыми и измеренной удельной теплотой. Чтобы получить полное определение удельной теплоты вещества, необходимо не только установить формы кривых удельной теплоты (цель, достижению которой помогает большая часть предыдущего обсуждения), но и определить температурную шкалу каждой кривой. Хотя теоретические выводы в связи с двумя теоретическими аспектами ситуации удельной теплоты, подобно всем выводам данной работы, выведены с помощью развития следствий фундаментальных постулатов теории Обратной Системы, они обязательно достигаются двумя линиями теоретического развития. По этой причине более значимое сравнение с экспериментальными данными может быть представлено, если мы имеем дело с двумя аспектами независимо. Поэтому в этой главе, экспериментальные величины будут графически сравниваться с теоретическими кривыми, с эмпирическими температурными шкалами. Глава 7 завершит определение кривых выведением релевантных температурных величин.
Рисунок 7: Удельная теплота
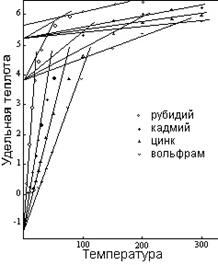
Кривые на рисунке 7 типичны для кривых большинства элементов.7 Как указывалось на рисунке 4, конечный, прямолинейный сегмент каждой кривой занимает большую часть температурной области твердого состояния в случае элементов с высокой точкой плавления. Следовательно, значимые характеристики кривых приспосабливаются к более низким температурам, и чтобы изобразить их яснее, на иллюстрациях показана только область более низкой температуры (до 300ºК). Оставшиеся сегменты кривых на рисунке 7 являются расширениями линий, показанных на графике, за исключением случая вольфрама, который подвергается переходу к статусу четырех единиц при температуре около 325ºК.
Рисунок 8 – это аналогичная группа кривых удельной теплоты для четырех электроотрицательных элементов с начальным уровнем –0,66. Кроме более высокого начального уровня, эти кривые идентичны кривым рисунка 7, когда все они понижены до обычной температурной шкалы. Переход к вибрации 2-х единиц происходит при величине 4,63 (2¹/3 R), невзирая на более высокий начальный уровень. Это положение будет рассматриваться подробнее в главе 7. Верхние части кривых свинца и сурьмы, не показанные на рисунке, являются расширениями линий на графике. Мышьяк и кремний обладают переходами при температурах выше 300ºК.
Рисунок 8: Удельная теплота
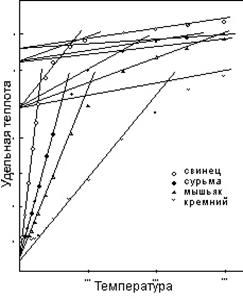
Как указывалось в главе 5, имеется ряд элементов, подвергающихся модификации температурной шкалы в точке первого перехода. Две кривые с модифицированным вторым сегментом показаны на рисунке 9.
Рисунок 9: Удельная теплота
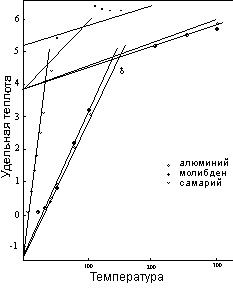
На самом деле, две кривые применимы к четырем элементам, поскольку удельная теплота лития следует кривой алюминия, в то время как рутений совпадает с кривой молибдена. Совпадение кривых удельной теплоты разных элементов, как в упомянутых примерах, не так уже необычно, как можно было бы ожидать. Число вероятных паттернов кривых довольно ограничено, и, как мы увидим в следующей главе, где будет исследоваться природа изменения в температуре, температурные коэффициенты согласуются с удельной теплотой в основном в относительно узкой области.
Также в рисунок 9 включен пример кривой удельной теплоты элемента, который подвергается внутренней реструктуризации, изменяющей температурный паттерн. Измерения, показанные для самария, следуют обычному паттерну вплоть до приближения к точке первого перехода при 35ºК. В этой точке, очевидно, начинается модификация молекулярной структуры, вместо перехода, или дополнение к обычному переходу в вибрационный статус двух единиц. Процесс поглощает значительное количество тепла, что проявляется как прибавление к измеренной удельной теплоте выше следующей части температурной области. При почти 175ºК регулировка завершается, и удельная теплота возвращается к обычной кривой. Большинство других редкоземельных элементов подвергается подобным регулировкам при сопоставимых температурах. Если где-то в другом месте происходят изменения такого рода, почти всегда они совершаются при относительно высоких температурах. Причина такой особенности редкоземельной группы еще не известна.
Рисунок 10: Удельная теплота – Водород
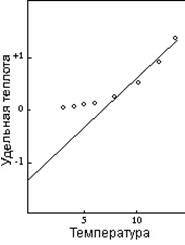
Все виды отклонений от нормального паттерна, обсужденные до сих пор, обнаруживаются у электроотрицательных элементов групп с более низким вращением. Имеется и дополнительный источник изменчивости удельной теплоты данных элементов, поскольку их атомы могут сочетаться друг с другом для формирования молекул. В результате существует достаточно широкое разнообразие поведения, обуславливающее уникальную кривую удельной теплоты почти для каждого элемента. Особое внимание привлекают случаи, когда измерение достигается за счет пропуска характеристик нормального паттерна. Например, кривая для неона – это единичная, прямая линия, начинающаяся с начального уровня –1,32 и продолжающаяся до точки плавления. Кривая удельной теплоты молекулы водорода, рисунок 10, - тоже прямая линия, но водород совсем не обладает компонентом удельной теплоты вращения, поэтому эта линия тянется лишь с отрицательного начального уровня –1,32 и продолжается до удельной теплоты положительного начального уровня +1,32, где находится точка плавления.
Удельная теплота бинарных соединений, основанных на обычной ориентации (это просто комбинации элементов Деления I и Деления IV), следует тому же паттерну, что и электроположительные элементы. У них каждый атом ведет себя как индивидуальная температурная единица, как это было бы в однородной совокупности одинаковых атомов. Молекулярная удельная теплота таких соединений в два раза больше величин, уже установленных для элементов, не потому что удельная теплота на атом другая, а потому что в каждой молекуле содержатся два атома.
Кривые для KCl и CaS, рисунок 11, иллюстрируют паттерн удельной теплоты данного класса соединений. На рисунке 11 также показаны некоторые бинарные соединения других структурных видов, соответствующие тому же нормальному паттерну.
Рисунок 11
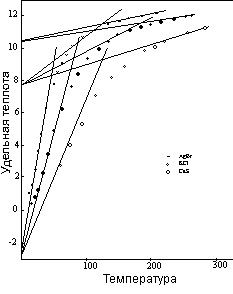
Поскольку у элементов тоже имеется отклонение от нормального паттерна, когда некоторые соединения электроотрицательных элементов обладают более высоким начальным уровнем, у соединений, таких как ZnO и SnO, этот уровень равен нулю, а не –0,66 как у элементов.
Некоторые большие молекулы температурно работают как объединения независимых атомов. Типичный пример - CaF2 and FeS2. Однако чаще два или более атомов, составляющих молекулы, действуют как одна температурная единица. Например, и молекула KHF2, состоящая из четырех атомов, и молекула CsClO4, состоящая из шести атомов, температурно действуют как три единицы. В последующем обсуждении для обозначения любой комбинации атомов, работающей как одна температурная единица, будет использоваться термин температурная группа. Там где индивидуальные атомы участвуют в температурном движении совместно с группами атомов, индивидуальные атомы будут называться моноатомными группами. На этом основании можно сказать, что в каждой из молекул KHF2 и CsClO4 имеются три температурные группы.
Огромное большинство соединений не только формируют температурные группы, но при изменении температуры меняют число групп в молекуле. Обычный паттерн иллюстрируется хлоридами хрома. При очень низких температурах CrCl2 действует как одна температурная группа, CrCl3 как две. Начальные уровни удельной теплоты соответственно –1,32 и –2,64. Вплоть до точки первого перехода происходит постепенное увеличение среднего числа температурных групп на молекулу, в точке перехода температура всех атомов работает независимо. В начальной точке второго сегмента кривой независимый статус поддерживается, а выше температуры перехода молекула CrCl2 действует как три температурные группы, а CrCl3 как четыре.
На нынешней стадии исследования, из теории, мы можем определить вероятные способы расщепления молекулы на температурные группы, но еще не можем указывать, какие из вероятностей будут превалировать при любой данной температуре, или где будет происходить переход от одной к другой. Однако уже разработанная теоретическая информация позволяет анализировать эмпирические данные и устанавливать паттерн удельной теплоты каждого вещества; то есть, определять, как оно будет температурно действовать. За исключением некоторых случаев, в основном включающих очень большие молекулы, где паттерн удельной теплоты необычно сложен, и в тех примерах, когда ошибки в экспериментах приводят к ошибочной интерпретации, можно определять действующее число температурных групп в важных точках кривых. Как только имеется информация для любого вещества, определение кривой удельной теплоты, по сути, завершено, за исключением температурной шкалы, определители которой будет обсуждаться в главе 7. Если число активных температурных групп соединения равно n, а начальный уровень –1,32 n, начальная точка второго сегмента кривой Типа 1 - 3,89 n, а точка первого перехода – 4,63 n.
Тенденция атомов многоатомных молекул формировать температурные группы особенно очевидна там, где молекулы содержат радикалы, за счет больших различий в силах сцепления, ответственных за существование радикалов. Степень, с которой естественно поддерживается объединение в температурные группы, зависит от относительной силы сцепления и силы разрушения. Такие радикалы, как ОН и СN, у которых связи очень сильные, действуют как единичные температурные группы при всех обычных условиях. Те же, у которых связи слабее (CO3, SO4, NO3 и так далее), действуют как одни единицы при более низких температурах. Таким образом, мы обнаруживаем, что в начальных точках первого и второго сегментов кривых удельной теплоты у MnCO3 имеются две группы, у Na2CO3 три группы, у KAl(SO4)2 четыре группы, у Ca3(PO4)2 пять групп и так далее. Однако при более высоких температурах радикалы этого класса расщепляются на две или более температурные группы. Еще более слабые радикалы, такие как ClO4, составляют две температурные группы даже при более низких температурах.
Как упоминалось в томе 1, пограничная линия между радикалами и группами независимых атомов довольно неопределенная. В общем, область силы связи, требующейся для структурного радикала, относительно велика, и мы находим много групп, осознаваемых как радикалы, кристаллизующиеся в такие структуры как куб CaTiO3, в котором радикал как таковой роли не играет. Область, требующаяся в температурном движении, намного меньше, особенно при низких температурах, и имеется много атомных групп, действующих температурно так же, как и опознанные радикалы. Например, у Li3CO3 два атома лития действуют как единичная температурная группа, и кривая удельной теплоты данного соединения похожа на кривую MgCO3, а не Na2CO3.
Расширение температурного движения посредством разрушения некоторых сильных связей при более высоких температурах приводит к увеличению разнообразия модификаций кривых удельной теплоты. Например, MoS2 имеет лишь две температурные группы в более низкой области, но как только температура поднимается, комбинация S2 распадается, и все атомы начинают вибрировать независимо. Аналогично, VCl2 образует из одной группы три. Распад радикала рассматривается как изменение из двух групп в три у SrCO3, из одной группы в три у AgNO3, из двух групп в шесть у (NH4)2SO4. Все эти изменения происходят в или до точки первого перехода. Другие соединения совершают первый переход на начальной основе и расщепляются на большее число температурных групп позже. В нормальном паттерне радикал, действующий как одна температурная группа при низких температурах, расщепляется на две группы в температурной области второго сегмента кривой, как делает это радикал у SrCO3, PbCO3 и других подобных соединений на более низком уровне. Имеется ряд структур, таких как KMnO4 и KIO3, у которых увеличение числа групп в молекулах происходит с двух до трех. У Pb3(PO4)2, имеющего два радикала, увеличение происходит с пяти групп до семи групп, и так далее.
Эффект кристаллизации воды меняется в зависимости от силы сцепления. Например, при низких температурах BaCl2 · 2H2O представляет собой три температурные группы, молекулы воды тесно связаны с атомами соединения. При повышении температуры связи ослабевают, и молекулы начинают вибрировать на основе пяти групп. У Al2(SO4)3.6H2O и NH4Al(SO4)2.12H2O связи с молекулами воды остаются фиксированными во всей области экспериментов вплоть до 300ºК; эти гидроокиси имеют соответственно пять и шесть температурных групп, как и у соответствующих безводных соединений.
На рисунке 12 показан пример значительного изменения температурного поведения за счет разрушения межатомных сил температурными силами. Радикал CrO3 в соединении AgCrO3 является единичной температурной группой при очень низких температурах. В температурной области до точки первого перехода происходит постепенное разделение на две группы, и изменение до вибрации двух единиц совершается на основе радикала, состоящего из двух групп. При температуре около 150ºК все четыре атома в радикале начинают вибрировать независимо, и молекула подвергается переходу из второго сегмента кривой для трех групп во второй сегмент кривой для пяти групп. При около 250ºК соединение совершает обычный переход к вибрации трех единиц, продолжая работать как пять температурных групп.
Используемые в качестве примеров соединения в основном выбирались на основе доступности экспериментальных данных в значимых температурных пределах. В целях точного определения наклона каждого из прямолинейных сегментов любой эмпирической кривой необходимо иметь измерения в температурной области, в которой отклонения за счет близости точки перехода незначительные. Примеры выбранных экспериментальных результатов удовлетворяют этому требованию.
Рисунок 12: Удельная теплота - AgCrO3
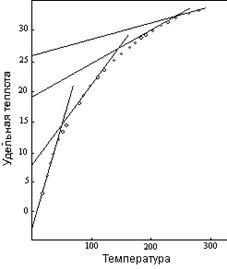
В теоретической трактовке удельной теплоты, такой как трактовка данной работы, приходится иметь дело с величиной на молекулу. Однако для практических целей удобнее пользоваться удельной теплотой на единицу массы, и большинство собранных данных выражаются именно таким способом. Следует заметить, что влияние объединения в температурные группы способствует уменьшению удельной теплоты на единицу массы. По этой причине при низких температурах удельная теплота большинства сложных соединений относительно низка, но повышается до величин, относящихся к индивидуальным атомам, когда повышение температуры расщепляет начальные температурные группы.
Самые простые органические соединения, состоящие из двух или трех структурных единиц, обычно делятся на не более чем две температурные группы. Многие большие органические молекулы, особенно среди кольцевых структур и ветвящихся соединений, следуют тому же правилу. Отношения удельной теплоты таких соединений подобны отношениям удельной теплоты неорганических соединений, за исключением того, что имеются органические соединения, у которых температурное движение ограничено одной единицей вращения. Подобные вещества, углеводороды и некоторые другие соединения более низких элементов, подвергаются переходу к положительному начальному уровню по достижении точки первого (и единственного) перехода. Результирующая кривая удельной теплоты (рисунок 3) не намного больше, чем прямая линия с изгибом. Несколько соединений, включая этан и угарный газ, даже упускают изгиб и не совершают переход к положительному начальному уровню.
Дальнейшее прибавление структурных единиц, таких как группы CH2, к простым органическим соединениям проявляется как активация внутренних температурных групп - единиц, температурно вибрирующих внутри молекул. Общая природа температурного движения внутренних групп идентична температурному движению молекулы в целом. Но внутренне движение не зависит от молекулярного температурного движения, а его скалярное направление (вовнутрь или наружу) не зависит от скалярного направления молекулярного движения. Таким образом, внутреннее движение наружу совпадает с молекулярным движением наружу только в течение четверти вибрационного цикла. Поскольку действующая величина температурного движения, которая определяется удельной теплотой, является скалярной суммой внутреннего и молекулярного компонентов, каждая единица внутреннего движения прибавляет половину единицы удельной теплоты в течение половины молекулярного цикла. Температурный эффект не влияет на вторую половину цикла, когда молекула в целом движется вовнутрь.
Из-за огромного многообразия органических соединений число паттернов удельной теплоты тоже велико. Влияние внутреннего движения в тех органических соединениях, в которых оно присутствует, хорошо проиллюстрировано удельной теплотой обычных парафинов. Величины начальных уровней и удельная теплота при T1 у соединений этой серии в области от C3 (пропана) до C16 (гексадекана) приведены в таблице 21, наряду с числом температурных единиц в молекуле каждого соединения.
Таблица 21: Удельная теплота - Парафиновые углеводороды
|
|
Внутр.темп. единицы |
|
Начальные уровни |
|
Удельная
теплота |
|
|
Пропан |
0 |
|
-2,64 |
|
2,64 |
9,27 |
|
Бутан |
0 |
|
-2,64 |
|
2,64 |
9,27 |
|
Пентан |
2 |
|
-2,64 |
|
6,62 |
13,90 |
|
Гексан |
3 |
|
-2,64 |
|
7,95 |
16,22 |
|
Гептан |
4 |
|
-3,96 |
|
9,27 |
18,54 |
|
Октан |
5 |
|
-3,96 |
|
1059 |
20,86 |
|
Нонан |
6 |
|
-5,30 |
|
11,92 |
23,18 |
|
Декан |
7 |
|
-5,30 |
|
13,24 |
25,49 |
|
Ундекан |
8 |
|
-5,30 |
|
14,57 |
27,81 |
|
Додекан |
9 |
|
-6,62 |
|
15,89 |
30,12 |
|
Тридекан |
10 |
|
-6,62 |
|
17,22 |
32,44 |
|
Тетрадекан |
11 |
|
-6,62 |
|
18,54 |
34,76 |
|
Пентадекан |
12 |
|
-6,62 |
|
19,86 |
37,08 |
|
Гексадекан |
13 |
|
-7,95 |
|
21,19 |
39,39 |
Пропан и бутан обладают лишь двумя молекулярными температурными группами, соответствующими положительному и отрицательному концу молекул, и их удельная теплота при T1 обладает обычной величиной двух групп: 9,27. Начиная с двух внутренних групп у пентана, происходит прибавление одной структурной группы CH2 и внутренней температурой единицы. Это прибавляет 2,317 к общей удельной теплоте молекулы в точке перехода. У более низких соединений, начальный уровень первого сегмента кривой удельной теплоты составляет –2,64 (величина двух групп), он медленно меняется, добавляя единицы –1,32, поскольку длина цепи увеличивается. Начальный уровень второго сегмента у бутана и пропана: 2,64. У более высоких соединений, каждое из которых состоит из n структурных групп (CH2 and CH3), второй начальный уровень составляет 1,324 n.
Таким образом, теоретические выведенные величины совпадают с экспериментальными кривыми. В некоторых случаях пересечение двух сегментов кривых может не совпадать с вычисленной удельной теплотой точки перехода, но эти отклонения, если реально существуют, достаточно малы для объяснения на основе изменений температурных коэффициентов, природа которых будет одним из вопросов, обсуждаемых в главе 7.
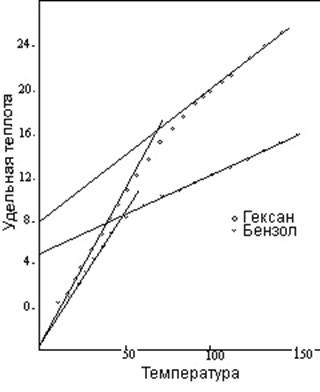
Ветвление цепи углеводорода уплотняет структуру и уменьшает число внутренних температурных единиц. Например, октан обладает пятью внутренними температурными единицами и удельной теплотой 20,86 в точке перехода. Но 2,2,4-триметил пентан, разветвленное соединение с тем же составом, совсем не обладает внутренним движением, и при T1 удельная теплота данного соединения составляет 9,27, идентично удельной теплоте парафина C3 - пропана. Кольцевое образование обладает аналогичным эффектом. Этил-бензол и ксилол, тоже являющиеся соединениями C8, обладают каким-то внутренним движением, но их удельная теплота при T1 составляет соответственно 11,59 (одна внутренняя единица) и 13,90 (две внутренние единицы), гораздо ниже уровня октана. На рисунке 13 сравниваются кривые удельной теплоты гексана (прямая цепь) и бензола (кольцо), оба они являются углеводородами C6.
Предмет обсуждения данной главы и пяти предыдущих глав состоит из разных аспектов объемных и температурных отношений материальных веществ. Изучение этих отношений являлось принципиальным подходом к прояснению основных физических процессов, что привело к определению физической вселенной как вселенной движения и определению природы фундаментальных характеристик этой вселенной. Отношения детально исследовались в течение многих лет; за эти годы были проанализированы и изучены тысячи экспериментальных результатов. Введение массы накопленной информации в теоретическую структуру стало первостепенной задачей, предпринятой после формулировки постулатов теории Обратной Системы. В результате, появилась возможность представления разумно законченного описания каждого обсужденного явления, включая то, что мы можем назвать мелкомасштабными эффектами.
Начиная со следующей главы, мы будем иметь дело с темами, не раскрытыми в период индуктивной фазы теоретического развития. Во второй фазе, дедуктивном развитии, мы расширяем применение теории на все другие важные области физической науки, чтобы продемонстрировать, что, по сути, она является общей физической теорией. Очевидно, там, где обсуждаемая область слишком обширна, ни один исследователь не может надеяться на осуществление дальнейшего развития в больших деталях. Соответственно, некоторые выводы, изложенные на последующих страницах в связи с мелкомасштабными характеристиками рассматриваемых областей, обладают определенной степенью неопределенности. В других случаях для будущего исследования понадобится опустить весь мелкомасштабный паттерн.
Рисунок 13: Удельная теплота
7 Данные удельной теплоты взяты в основном у Hultgren, et al, Selected Values of the Thermodynamic Properties of the Elements, American Society for Metals, Metals Park, OH, 1973, и Thermophysical Properties of Matter, Vol. 4, Touloukian and Buyko, editors, IFI Plenum Data Co., New York, 1970, с некоторыми дополнительными данными из оригинальных источников.
